O Problema do Caixeiro Viajante (PCV), ou Travelling Salesman Problem em inglês, pode parecer um quebra-cabeça matemático distante, mas sua aplicação prática pode transformar sua próxima viagem em uma aventura otimizada. Por otimizada, queremos dizer que você gastaria a menor distância e tempo para percorrer todos os lugares turísticos de um determinado local.
Imagine o PCV como um guia mágico que planeja o caminho mais eficiente para explorar diversas cidades ou pontos turísticos, economizando tempo e energia. Vamos desbravar esse mistério e descobrir como ele pode ser um aliado valioso para qualquer viajante. Porém, já fique sabendo que este é um problema bem difícil de ser resolvido, mesmo com nossos computadores super potentes.
O que é o problema do caixeiro viajante?
O PCV desafia a encontrar o caminho mais curto que visita todas as cidades (ou localizações) desejadas e retorna ao ponto de partida. Embora inicialmente tenha surgido como um quebra-cabeça matemático, sua relevância prática tornou-se evidente em diversas áreas, desde logística até a otimização de rotas de entregas e, claro, o planejamento de viagens.
Por que ele é tão desafiador?
A complexidade do PCV reside na busca pela melhor rota entre cidades, que se torna incrivelmente complicada à medida que o número de destinos aumenta. Esse desafio se traduz em dificuldades computacionais, tornando o PCV um problema NP-difícil (ou NP-hard, ou NP-complexo), o que significa que não há solução rápida e direta para todos os casos.
Para explicar melhor sobre um problema NP-difícil de forma simples, citamos o site do Instituto de Matemática e Estatística da USP (IME-USP), que diz: “a complexidade de um problema computacional é o consumo de tempo do melhor algoritmo possível para o problema”. Então, um problema NP-difícil é um problema que consome bastante tempo para tentar encontrar uma solução aceitável.
Falaremos mais sobre a complexidade do problema logo a frente.
Breve contexto histórico
O PCV tem suas raízes em propostas antigas, mas sua evolução ao longo do tempo o transformou em uma peça fundamental da teoria dos grafos. Matemáticos como Sir William Rowan Hamilton e Thomas Penyngton Kirkman contribuíram para moldar sua forma moderna.
De forma simples, digamos que grafos são uma coleção de pontos e linhas que se conectam entre eles. Parece complicado, mas veja a imagem abaixo com um exemplo de três pontos turísticos:
Como aplicar o Problema do Caixeiro Viajante em suas viagens?
Imagine planejar uma viagem pela Europa, visitando várias cidades. Ao invés de confiar apenas na intuição, você pode usar algoritmos inspirados no PCV para otimizar seu itinerário. Ferramentas online, como o Google Maps, podem ajudar a calcular as rotas mais eficientes e economizar tempo valioso durante sua jornada.
Então, a ideia geral é que você defina, a partir de um ponto de partida e chegada, os locais que você quer visitar. Com isso definido, o próximo passo é calcular qual seria a rota mais eficiente e rápida para percorrer todos os pontos de interesse. Digamos que a gente já tenta fazer isso de cabeça, sempre pensando “se estamos aqui, vamos para ali e depois para lá para não perder tanto tempo e reduzir a caminhada”. Mas, usando algoritmos e computadores, a otimização dessa rota fica excelente.
Exemplo prático
Suponha que você esteja em Paris e queira visitar três pontos turísticos, como no grafo mostrado logo acima, porém vamos dar nome aos pontos, sendo eles: o Museu do Louvre, a Torre Eiffel e o Arco do Triunfo. Utilizando princípios do PCV, você pode criar um itinerário eficiente que minimiza a distância total percorrida, permitindo que você aproveite ao máximo sua visita.
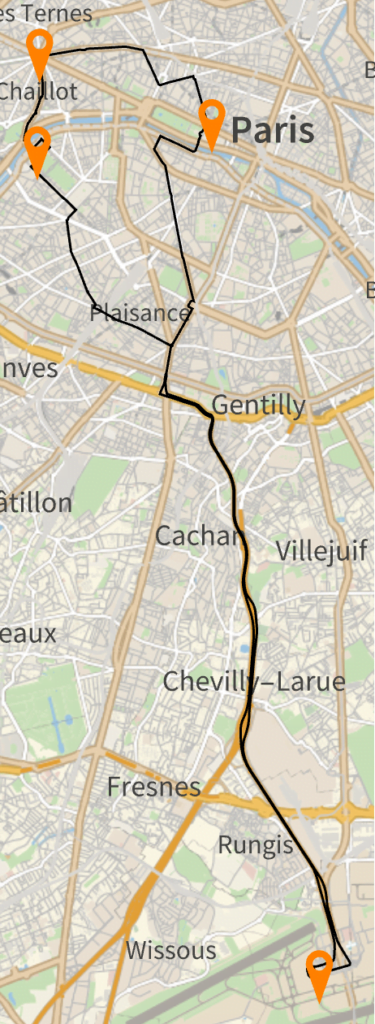
Digamos que a gente vai iniciar e finalizar o nosso tour a partir do Aeroporto de Paris-Orly (o marcador logo fim do mapa). Colocamos o aeroporto como início e fim do tour e iniciamos um algoritmo qualquer para gerar a rota mais eficiente para a gente.
Geramos um mapa de acordo com o algoritmo que usamos para gerar a rota mais eficiente. Nesse exemplo, nosso tour ficaria da seguinte forma:
Saída do Aeroporto de Paris-Orly -> Torre Eiffel -> Arco do Triunfo -> Museu do Louvre -> Volta ao Aeroporto.
Esse exemplo não é tão complexo, pois usamos cinco pontos, o de partida e saída e os três pontos turísticos. Mas, como falamos no início do texto, a complexidade e o consumo de tempo para resolver um algoritmo e trazer a rota mais otimizada vai aumentar de acordo com que aumentamos o número de pontos (os locais que queremos visitar).
Nesse caso de três pontos turísticos, podemos usar um algoritmo simples e resolver em questão de segundos. Porém, se a gente quiser usar um algoritmo de PCV para otimizar uma rota com 20 pontos turísticos usando um computador veloz, de acordo com o texto publicado pelo J.F. Porto da Silveira, no site do Instituto de Matemática e Estatística da Universidade Federal do Rio Grande do Sul (IME-UFRGS), isso demoraria 73 anos. Porém, temos que levar em conta que o texto foi publicado nos anos 2000 e que já temos computadores muito mais potentes hoje em dia. De qualquer forma, mesmo se demorar um terço desse tempo, ainda seria um problema bem complexo e que consumiria bastante tempo.
Conclusão
O Problema do Caixeiro Viajante não é apenas uma curiosidade matemática; é uma ferramenta prática para otimizar itinerários de viagem. Ao explorar seus princípios, podemos transformar nossas viagens mais e deixá-las mais eficientes e memoráveis. Mas, lembre-se que viajar é um momento de descontração, descanso e prazer.
Então, da próxima vez que estiver planejando o seu roteiro, na sua cabeça, usando o Notion, ChatGPT ou até mesmo com a ajuda de algum algoritmo, lembre-se do Caixeiro Viajante como seu aliado na busca pelo caminho perfeito e aproveite a sua viagem!
Continue lendo
- Pergunta para prática da OBL (Olimpiada Brasileira de Informática) https://olimpiada.ic.unicamp.br/pratique/ps/2020/f2/caixeiro/
- Livro: https://www.amazon.com/exec/obidos/ASIN/0471904139/ref=nosim/ericstreasuretro
- MathWorld: https://mathworld.wolfram.com/TravelingSalesmanProblem.html
- Wikipedia: https://en.wikipedia.org/wiki/Travelling_salesman_problem



Deixe um comentário